第 5 讲 一元函数微分学的几何应用

一、极值与最值的概念

定义 1    若存在 $x_0$ 的某个邻域，使得在该邻域内任意一点 x，均有 $f(x)\le f(x_0)(\mathrm{或}f(x)\ge f(x_0)$ 成立，则称 $x_0$ 为 $f(x)$ 的广义的极大值点（或极小值点），$f(x_0)$ 为 $f(x)$ 的广义的极大值（或极小值）。

定义 2    若存在 $x_0$ 的某个去心邻域，使得对于该邻域内任一异于 $x_0$ 的点 x，均有 $f(x)<f(x_0)(\mathrm{或}f(x)>f(x_0)$ 成立，则称 $x_0$ 为 $f(x)$ 的真正的极大值点（或极小值点），$f(x_0)$ 为 $f(x)$ 的真正的极大值（或极小值）。

定义 3    设 $x_0$ 为 $f(x)$ 定义域内一点，若对于 $f(x)$ 的定义域内任意一点 x，均有 $f(x)\le f(x_0)(\mathrm{或}f(x)\ge f(x_0))$ 成立，则称 $f(x_0)$ 为 $f(x)$ 的广义的最大值（或最小值）。

定义 4    设 $x_0$ 为 $f(x)$ 定义域内一点，若对于 $f(x)$ 的定义域内任一异于 $x_0$ 的点 x，均有 $f(x)<f(x_0)(\mathrm{或}f(x)>f(x_0))$ 成立，则称 $f(x_0)$ 为 $f(x)$ 的真正的最大值（或最小值）。

【注】（1）极值点并不一定是最值点，最值点也不一定是极值点

如果 $f(x)$ 在区间 $I$ 上有最值点 $x_0$，并且此最值点 $x_0$ 不是区间 $I$ 的端点而是 $I$ 内部的点，那么此 $x_0$ 必是 $f(x)$ 的一个极值点。

（2）间断点也可以是极值点

二、单调性与极值的判别

1. 单调性的判别

若用导数工具，则若 $y=f(x)$ 在区间 $I$ 上有 $f^{\prime }(x)>0$，则 $y=f(x)$ 在 $I$ 上严格单调增加；相应地，若 $y=f(x)$ 在区间 $I$ 上有 $f^{\prime }(x)<0$，则 $y=f(x)$ 在 $I$ 上严格单调减少。

2. 一阶可导点是极值点的必要条件

设 $f(x)$ 在 $x=x_0$ 处可导，且在点 $x_0$ 处取得极值，则必有 $f^{\prime }(x_0)=0$。

3. 判别极值的第一充分条件

设 $f(x)$ 在 $x=x_0$ 处连续，且在 $x_0$ 的某去心邻域 $\mathring{U}(x_0,\delta )$ 内可导

① 若 $x\in (x_0-\delta ,x_0)$ 时，$f^{\prime }(x)<0$，而 $x\in (x_0,x_0+\delta )$ 时，$f^{\prime }(x)>0$，则 $f(x)$ 在 $x=x_0$ 处取得极小值

② 若 $x\in (x_0-\delta ,x_0)$ 时，$f^{\prime }(x)>0$，而 $x\in (x_0,x_0+\delta )$ 时，$f^{\prime }(x)<0$，则 $f(x)$ 在 $x=x_0$ 处取得极大值

③ 若 $f^{\prime }(x)$ 在 $(x_0-\delta ,x_0)$ 和 $(x_0,x_0+\delta )$ 内不变号，则点 $x_0$ 不是极值点。

4. 判别极值的第二充分条件

设 $f(x)$ 在 $x=x_0$ 处二阶可导，且 $f^{\prime }(x_0)=0,f^{″}(x_0)\ne 0$

① 若 $f^{″}(x_0)<0$，则 $f(x)$ 在 $x=x_0$ 处取得极大值

② 若 $f^{″}(x_0)>0$，则 $f(x)$ 在 $x=x_0$ 处取得极小值

上述第二充分条件可以推广为第三充分条件

5. 判别极值的第三充分条件

设 $f(x)$ 在 $x=x_0$ 处 n 阶可导，且 $f^{(m)}(x_0)=0(m=1,2,\cdots ,n-1),f^{(n)}(x_0)\ne 0(n\ge 2)$，则

① 当 n 为偶数且 $f^{(n)}(x_0)<0$ 时，$f(x)$ 在 $x_0$ 处取得极大值

② 当 n 为偶数且 $f^{(n)}(x_0)>0$ 时，$f(x)$ 在 $x_0$ 处取得极小值

【注】上述第三充分条件的证明如下：由于 n 为偶数，令 n=2k，构\造极限

$$\begin{gathered} \underset{x\to x_0}{lim}\frac{f(x)-f(x_0)}{(x-x_0{)}^{2k}}\stackrel{\mathrm{洛}\mathrm{必}\mathrm{达}\mathrm{法}\mathrm{则}}{=}\underset{x\to x_0}{lim}\frac{f^{\prime }(x)}{2k(x-x_0{)}^{2k-1}}\stackrel{\mathrm{洛}\mathrm{必}\mathrm{达}\mathrm{法}\mathrm{则}}{=}\cdots \stackrel{\mathrm{洛}\mathrm{必}\mathrm{达}\mathrm{法}\mathrm{则}}{=}\underset{x\to x_0}{lim}\frac{f^{(2k-1)}(x)}{(2k)!(x-x_0)} \\ =\underset{x\to x_0}{lim}\frac{f^{(2k-1)}(x)-f^{(2k-1)}(x_0)}{(2k)!(x-x_0)}=\frac{1}{(2k)!}{f}^{(2k)}(x_0)\ne 0 \end{gathered}$$

上述洛必达法则成立的依据是，最后的结果 $\frac{1}{(2k)!}{f}^{(2k)}(x_0)$ 是存在的。

当 $f^{(2k)}(x_0)<0$ 时，由函数极限的局部保号性 $\Rightarrow \frac{f(x)-f(x_0)}{(x-x_0{)}^{2k}}<0\Rightarrow f(x)<f(x_0)$，故 $x_0$ 为极大值点

当 $f^{(2k)}(x_0)>0$ 时，由函数极限的局部保号性 $\Rightarrow \frac{f(x)-f(x_0)}{(x-x_0{)}^{2k}}>0\Rightarrow f(x)>f(x_0)$，故 $x_0$ 为极小值点

三、凹凸性与拐点的概念

1. 凹凸性的定义

设函数 $f(x)$ 在区间 $I$ 上连续。如果对 $I$ 上任意 $x_1,x_2$ 两点，恒有 $f(\frac{x_1+x_2}{2}）<\frac{f(x_1)+f(x_2)}{2}$，则 称 $y=f(x)$ 在 $I$ 上的图形是凹的（或凹弧），如图 1-5-1(a) 所示；如果恒有 $f(\frac{x_1+x_2}{2}）>\frac{f(x_1)+f(x_2)}{2}$，则 称 $y=f(x)$ 在 $I$ 上的**图形是凸的（或凸弧）**如图 1-5-1(b) 所示；

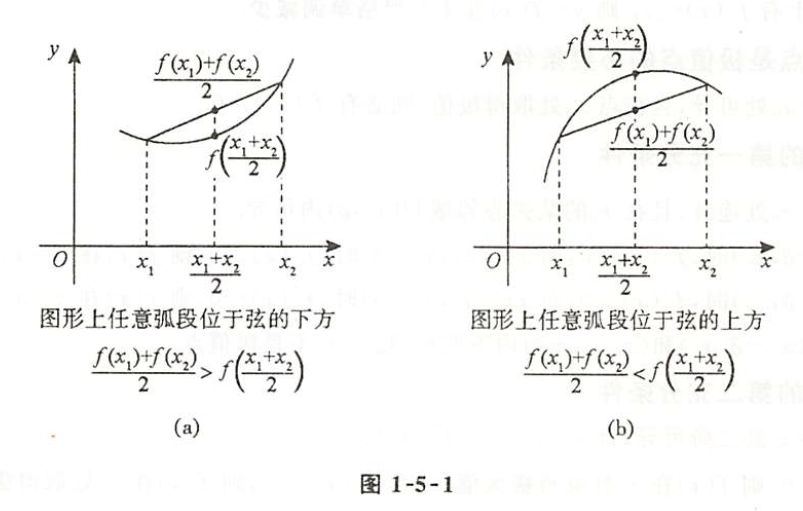
2. 拐点定义

连续曲线的凹弧与凸弧的分界点称为该曲线的拐点

四、凹凸性与拐点的判别

1. 判断凹凸性

设函数 $f(x)$ 在 $I$ 上二阶可导

① 若在 $I$ 上 $f^{″}(x)>0$，则 $f(x)$ 在 $I$ 上的图形是凹的

② 若在 $I$ 上 $f^{″}(x)<0$，则 $f(x)$ 在 $I$ 上的图形是凸的

2. 二阶可导点是拐点的必要条件

设 $f^{″}(x_0)$ 存在，且点 $(x_0,f(x_0))$ 为曲线上的拐点，则 $f^{″}(x_0)=0$

3. 判别拐点的第一充分条件

设 $f(x)$ 在点 $x=x_0$ 处连续，在点 $x=x_0$ 的某去心邻域 $\mathring{U}(x_0,\delta )$ 内存在二阶导数存在，且在该点的左、右邻域内 $f^{″}(x)$ 变号（无论是由正变负，还是由负变正），则点 $(x_0,f(x_0))$ 为曲线上的拐点

【注】$(x_0,f(x_0))$ 为曲线 $y-f(x)$ 上的拐点时，并不要求 $f(x)$ 在点 $x_0$ 的导数存在，如 $y=\sqrt[3]{x}$ 在 $x=0$ 的情形

4. 判别拐点的第二充分条件

设 $f(x)$ 在 $x=x_0$ 的某邻域内三阶可导，且 $f^{″}(X_0)=0,f^{‴}(x_0)\ne 0$，则 $(x_0,f(x_0))$ 为拐点

5. 判别拐点的第三充分条件

设 $f(x)$ 在 $x_0$ 处 n 阶可导，且 $f^{(m)}(x_0)=0(m=2,\cdots ,n-1),f^{(n)}(x_0)\ne 0(n\ge 3)$，则当 n 为奇数时，$(x_0,f(x_0))$ 为拐点

【注 1】上述第三充分条件的证明如下：由于 n 为奇数，令 n=2k+1，构造极限

$$\begin{gathered} \underset{x\to x_0}{lim}\frac{f^{″}(x)}{(x-x_0{)}^{2k-1}}\stackrel{\mathrm{洛}\mathrm{必}\mathrm{达}\mathrm{法}\mathrm{则}}{=}\cdots \stackrel{\mathrm{洛}\mathrm{必}\mathrm{达}\mathrm{法}\mathrm{则}}{=}\underset{x\to x_0}{lim}\frac{f^{(2k)}(x)}{(2k-1)!(x-x_0)} \\ =\underset{x\to x_0}{lim}\frac{f^{(2k)}(x)-f^{(2k)}(x_0)}{(2k-1)!(x-x_0)}=\frac{1}{(2k-1)!}{f}^{(2k+1)}(x_0)\ne 0 \end{gathered}$$

上述洛必达法则成立的依据是，最后的结果 $\frac{1}{(2k-1)!}{f}^{(2k+1)}(x_0)$ 是存在的。

当 $f^{(2k+1)}(x_0)>0$ 式，由函数极限的局部保号性，得 $\frac{f^{″}(x)}{(x-x_0{)}^{2k-1}}>0$

当 $x\to x_0^{+}$ 时，$f^{″}(x)>0$；当 $x\to x_0^{-}$ 时，$f^{″}(x)<0$，故 $(x_0,f(x_0))$ 为拐点

【注 2】由上述证明过程可知，第三充分条件不需要 $f^{\prime }(x_0)=0$ 这个条件

五、渐进性

1. 铅锤渐近线

若 $\underset{x\to x_0^{+}}{lim}f(x)=\mathrm{\infty }(\mathrm{或}\underset{x\to x_0}{lim}f(x)=\mathrm{\infty })$，则 $x=x_0$ 为一条铅锤渐近线

【注】此处的 $x_0$ 一般是函数的无定义点

2. 水平渐近线

若 $\underset{x\to +\mathrm{\infty }}{lim}f(x)=y_1$，则 $y=y_1$ 为一条水平渐近线；若 $\underset{x\to -\mathrm{\infty }}{lim}f(x)=y_2$，则 $y=y_2$ 为一条水平渐近线；

若 $\underset{x\to +\mathrm{\infty }}{lim}f(x)=\underset{x\to -\mathrm{\infty }}{lim}f(x)=y_0$，则 $y=y_0$ 为一条水平渐近线

3. 斜渐近线

若 $\underset{x\to +\mathrm{\infty }}{lim}\frac{f(x)}{x}=k_1,\underset{x\to +\mathrm{\infty }}{lim}[f(x)-k_{1}x]=b_1$，则 $y=k_{1}x+b_1$ 是曲线 $y=f(x)$ 的一条斜渐近线

若 $\underset{x\to -\mathrm{\infty }}{lim}\frac{f(x)}{x}=k_2,\underset{x\to -\mathrm{\infty }}{lim}[f(x)-k_{2}x]=b_2$，则 $y=k_{2}x+b_2$ 是曲线 $y=f(x)$ 的一条斜渐近线

若 $\underset{x\to +\mathrm{\infty }}{lim}\frac{f(x)}{x}=\underset{x\to -\mathrm{\infty }}{lim}\frac{f(x)}{x}=k,\underset{x\to +\mathrm{\infty }}{lim}[f(x)-kx]-\underset{x\to -\mathrm{\infty }}{lim}[f(x)-kx]=b$，则 $y=kx+b$ 是曲线 $y=f(x)$ 的一条斜渐近线

六、最值或取值范围

1. 求闭区间 [a, b] 上连续函数 $f(x)$ 的最大值 M 和最小值 m

① 求出 $f(x)$ 在 $(a,b)$ 内的可疑点——驻点与不可导点，并求出这些可疑点处的函数值

② 求出端点的函数值 $f(a)$ 和 $f(b)$

③ 比较以上所求得的所有函数值，其中最大者为 $f(x)$ 在 [a, b] 上的最大值 M，最小者为 $f(x)$ 在 [a, b] 上的最小值 m

2. 求开区间 (a, b) 内连续函数 $f(x)$ 的最值或取值范围

① 求出 $f(x)$ 在 (a, b) 内的可疑点——驻点与不可导点，并求出这些可疑点处的函数值

② 求 (a, b) 两端的单侧极限：若 a, b 为有限常数，则求 $\underset{x\to a^{+}}{lim}f(x)$ 与 $\underset{x\to b^{-}}{lim}f(x)$；若 a 为 $-\mathrm{\infty }$，则求 $\underset{x\to -\mathrm{\infty }}{lim}f(x)$，若 b 为 $+\mathrm{\infty }$，则求 $\underset{x\to +\mathrm{\infty }}{lim}f(x)$。记以上所求左端极限为 A，右端极限为 B

③ 比较 ①，② 所得结果，确定最值或取值范围

七、作函数图形

给出函数 $f(x)$，作图的一般步骤：

① 确定函数 $f(x)$ 的定义域，并考查它是否有奇偶对称性

② 求出 $f^{\prime }(x),f^{″}(x)$，用 $f(x)$ 的无定义点，$f^{\prime }(x)=0$ 的点，$f^{\prime }(x)$ 不存在的点，$f^{″}(x)=0$ 的点，$f^{″}(x)$ 不存在的点，将定义域划分为若干子区间，确定函数图形在各个子区间上的单调性与凹凸性，进而确定函数的极值点和拐点

③ 确定渐近线（如果有的话）

④ 作出函数图形