408 真题
**【2009 统考真题】**已知一个带有表头结点的单链表,结点结构为
假设该链表只给出了头指针 list。在不改变链表的前提下,请设计一个尽可能高效的算法,查找链表中倒数第 k 个位置上的结点(k 为正整数)。若查找成功,算法输出该结点的 data 域的值,并返回 1;否则,只返回 0。要求:
1)描述算法的基本设计思想。
2)描述算法的详细实现步骤。
3)根据设计思想和实现步骤,采用程序设计语言描述算法(使用 C、C++ 或 Java 语言实现),关键之处请给出简要注释。
【解答】
1)算法的基本设计思想如下:
问题的关键是设计一个尽可能高效的算法,通过链表的一次遍历,找到倒数第 k 个结点的位置。算法的基本设计思想是:定义两个指针变量 p 和 q,初始时均指向头结点的下一个结点(链表的第一个结点),p 指针沿链表移动;当 p 指针移动到第 k 个结点时,q 指针开始与 p 指针同步移动;当 p 指针移动到最后一个结点时,q 指针所指示的结点为导数第 k 个结点。以上过程对链表仅进行一遍扫描。
2)算法的详细实现步骤如下:
① count=0,p 和 q 指向链表表头结点的下一个结点。
② 若 p 为空,转 ⑤。
③ 若 count 等于 k,则 q 指向下一个结点;否则,count++。
④ p 指向下一个结点,转 ②。
⑤ 若 count 等于 k,则查找成功,输出该结点的 data 域的值,返回 1;否则,说明 k 值超过了线性表的长度,查找失败,返回 0.
⑥ 算法结束。
3)算法实现如下:
typefef int ElemType; // 链表数据的类型定义
tyedef struct LNode{ // 链表结点的结构定义
ElemType data; // 结点数据
struct LNOde *link; // 结点链接指针
}LNode,*LinkList;
int Search_k(LinkList list, int k){
LNode *p=list->link;*q=list->link; // 指针p、q指示第一个结点
int count=0;
while(p!=NULL){ // 遍历链表直到最后一个结点
if(count<k) count++; // 计数,若count<k只移动p
else q=q->link;
p=p->link; // 之后让p、q同步移动
}//while
if(count<k)
return 0; // 查找失败返回0
else{ // 否则打印并返回1
printf("%d",q->data);
return 1;
}
}**【2010 统考真题】**设将 n(n>1) 个整数存放到一维数组 R 中。设计一个在时间和空间两方面都尽可能高效的算法。将 R 中保存的序列循环左移 p(0<p<n) 个位置,即将 R 中的数据由
1)给出算法的基本设计思想。
2)根据设计思想,采用 C 或 C++ 或 Java 语言描述算法,关键之处给出注释。
3)说明你所设计算法的时间复杂度和空间复杂度。
【解答】
1)算法的基本设计思想:
可将问题视为把数组 ab 转换成数组 ba(a 代表数组的前 p 个元素,b 代表数组中余下的 n-p 个元素),先将 a 逆置得到 a-1b,再将 b 逆置 得到 a-1b-1,最后将整个 a-1b-1 逆置得到 (a-1b-1)-1=ba。设 Reverse 函数执行将数组逆置的操作,对 abcdefgh 向左循环 3(p=3) 个位置的过程如下:
Reverse(0, p-1) 得到 cbadefgh
Reverse(p, n-1) 得到 cbahgfed
Reverse(0, n-1) 得到 defghabc
2)使用 C 语言描述算法如下:
void Reverse(int R[], int from, int to){
int i, temp;
for(i=0; i<(to-from+1)/2; i++){
temp = R[from+i];
R[from+i]=R[to-i];
R[to-i]=temp;
}
}//Reverse
void Coverse(int R[], int n, int p){
Reverse(R, 0, p-1);
Reverse(R, p, n-1);
Reverse(R, 0, n-1);
}3)上述算法中三个 Reverse 函数的时间复杂度分别为
【2011 统考真题】一个长度为 L(L≥1) 的升序序列 S,处在第
1)给出算法的基本设计思想。
2)根据设计思想,采用 C 或 C++ 或 Java 语言描述算法,关键之处给出注释。
3)说明你所设计算法的时间复杂度和空间复杂度。
【解答】
1)算法的基本设计思想如下。
分别求两个升序序列 A、B 的中位数,设为 a 和 b,求序列 A、B 的中位数过程如下:
① 若 a = b,则 a 或 b 即为所求中位数,算法结束。
② 若 a < b,则舍弃序列 A 中较小的一半,同时舍弃序列 B 中较大的一半,要求两次舍弃的长度相等。
③ 若 a > b,则舍弃序列 A 中较大的一半,同时舍弃序列 B 中较小的一半,要求两次舍弃的长度相等。
在保留的两个升序序列中,重复过程 ①、②、③,直到两个序列中均只含一个元素时为止,较小者即为所求的中位数。
2)本题代码如下:
int M_Search(int A[], int B[], int n){
int s1=0,d1=n-1,m1,s2=0,d2=n-1,m2;
// 分别表示序列 A 和 B 的首位数、末位数和中位数
while(s1!=d1 || s2!=d2){
m1=(s1+d1)/2;
m2=(s2+d2)/2;
if(A[m1]==B[m2])
return A[m1]; // 满足条件 ①
if(A[m1]<B[m2]){ // 满足条件 ②
if((s1+d1)%2==0){ // 若元素个数为奇数
s1=m1; // 舍弃 A 中间点以前的部分且保留中间点
d2=m2; // 舍弃 B 中间点以后的部分且保留中间点
}
else{ // 元素个数为偶数
s1=m1+1; // 舍弃 A 中间点及中间点以前部分
d2=m2; // 舍弃 B 中间点以后部分且保留中间点
}
}
else{ // 满足条件 ③
if((s2+d2)%2==0){ // 若元素个数为奇数
d1=m1; // 舍弃 A 中间点以前的部分且保留中间点
s2=m2; // 舍弃 B 中间点以后的部分且保留中间点
}
else{ // 元素个数为偶数
d1=m1; // 舍弃 A 中间点以后部分且保留中间点
s2=m2+1; // 舍弃 B 中间点及中间点以前部分
}
}
}
return A[s1]<B[s2] ? A[s1] : B[s2];
}3)算法的时间复杂度为
**【2012 统考真题】**假定采用带头结点的单链表保存单词,当两个单词有相同的后缀时,可共享相同的后缀存储空间,例如,loading 和 being 的存储映射如下图所示。
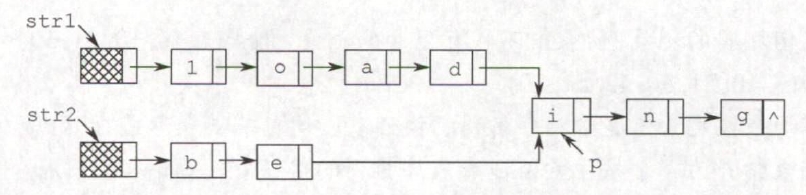
设 str1 和 str2 分别指向两个单词所在单链表的头结点,链表结点结构为
1)给出算法的基本设计思想。
2)根据设计思想,采用 C 或 C++ 或 Java 语言描述算法,关键之处给出注释。
3)说明你所设计算法的时间复杂度和空间复杂度。
【解答】
本题的结构体是单链表,采用双指针法。用指针 p、q 分别扫描 str1 和 str2,当 p、q 指向同一个地址时,即找到共同后缀的起始位置。
1)算法的基本设计思想如下:
① 分别求出 str1 和 str2 所指的两个链表的长度 m 和 n。
② 将两个链表以表尾对齐:令指针 p、q 分别指向 str1 和 str2 的头结点,若 m≥n,则指针 p 先走,使 p 指向链表中的第 m-n+1 个结点;若 m<n,则使 q 指向链表中的第 n-m+1 个结点,即使指针 p 和 q 所指的结点到表尾的长度相等。
③ 反复将指针 p 和 q 同步向后移动,当 p、q 指向同一位置时停止,即为共同后缀的起始位置,算法结束。
2)本题代码如下:
typedef struct Node{
char data;
struct Node *next;
}SNode;
/* 求链表长度的函数 */
int listlen(SNode *head){
int len=0;
while(head->next!=NULL){
len++;
head=head->next;
}
return len;
}
/* 找出共同后缀的起始地址 */
SNode* find_addr(SNode *str1, SNode *str2){
int m,n;
SNode *p,*q;
m=listlen(str1); // 求str1的长度
n=listlen(str2); // 求str2的长度
for(p=str1;m>n;m--) // 若m>n,使p指向链表中的第m-n+1个结点
p=p->next;
for(q=str2;m<n;n--) // 若m<n,使q指向链表中的第m-n+1个结点
q=q->next;
while(p->next!=NULL && p->next!=q->next){ // 将指针p和q同步向后移动
p=p->next;
q=q->next;
}
return p->next; // 返回共同后缀的起始地址
}3)时间复杂度为
**【2013 统考真题】**已知一个整数序列
1)给出算法的基本设计思想。
2)根据设计思想,采用 C 或 C++ 或 Java 语言描述算法,关键之处给出注释。
3)说明你所设计算法的时间复杂度和空间复杂度。
【解答】
1)算法的基本设计思想:算法的策略是从前向后扫描数组元素,标记出一个可能成为主元素的元素 Num。然后重新计数,确认 Num 是否是主元素。
算法可分为以下两步:
① 选取候选的主元素。依次扫描所给数据中的每个整数,将第一个遇到的整数保存到 c 中,记录 Num 的出现次数为 1;若遇到的下一个整数仍等于 Num,则计数加 1,否则计数减 1;当计数减到 0 时,将遇到的下一个整数保存到 C 中,计数重新记为 1,开始新一轮计数,即从当前位置开始重复上述过程,直到扫描完全部数组元素。
② 判断 c 中元素是否是真正的主元素。再次扫描该数组,统计 c 中元素出现的次数,若大于 n/2,则为主元素;否则,序列中不存在主元素。
2)算法实现如下:
int Majority(int A[], int n){
int i, c, count=1; // c用来保存候选主元素,count用来计数
c=A[0]; // 设置A[0]为候选主元素
for(i=1; i<n; i++) // 查找候选主元素
if(A[i]==c)
count++; // 对A中的候选主元素计数
else
if(count>0) // 处理不是候选主元素的情况
count--;
else{ // 更换候选主元素,重新计数
c=A[i];
count=1;
}
if(count>0)
for(i=count=0; i<n; i++) // 统计候选主元素的实际出现次数
if(A[i]==c)
count++;
if(count>n/2) return c; // 确认候选主元素
else return -1; // 不存在主元素
}3)实现的程序的时间复杂度为
**【2014 统考真题】**二叉树的带权路径长度(WPL)是二叉树中所有叶结点的带权路径长度之和。给定一棵二叉树 T,采用二叉链表存储,结点结构为
1)给出算法的基本设计思想。
2)使用 C 或 C++ 语言,给出二叉树结点的数据类型定义。
3)根据设计思想,采用 C 或 C++ 或 Java 语言描述算法,关键之处给出注释。
【解答】
考查二叉树的带权路径长度,二叉树的带权路径长度为每个叶结点的深度与权值之积的总和,可以使用先序遍历或层次遍历解决问题。
1)算法的基本设计思想。
① 基于先序递归遍历的算法思想是用一个 static 变量记录 wpl,把每个结点的深度作为递归函数的参数传递,算法步骤如下:
· 若该结点是叶结点,则 wpl 加上该结点的深度与权值之积。
· 若该结点是非叶结点,则左子树不为空时,对左子树调用递归算法,右子树不为空,对右子树调用递归算法,深度参数均为本结点的深度参数加 1.
· 最后返回计算出的 wpl 即可。
② 基于层次遍历的算法思想是使用队列进行层次遍历,并记录当前的层数:
· 当遍历到叶结点时,累计 wpl。
· 当遍历到非叶结点时,把该结点的子树加入队列。
· 当某结点为该层的最后一个结点时,层数自增 1。
队列空时遍历结束,返回 wpl。
2)二叉树结点的数据类型定义如下。
tyedef struct BiTNode{
int weight;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;3)算法的代码如下:
① 基于先序遍历的算法:
int WPL(BiTree root){
return wpl_PreOrder(root,0);
}
int wpl_PreOrder(BiTree root, int deep){
static int wpl=0; // 定义变量存储wpl
if(root->lichild==NULL&&root->rchild==NULL) // 若为叶结点,则累积wpl
wpl+=deep*root->weight;
if(root->lchild!=NULL) // 若左子树不空,则对左子树递归遍历
wpl_PreOrder(root->lchild,deep+1);
if(root->chilid!=NULL) // 若右子树不空,则对右子树递归遍历
wpl_PreOrder(root->rchild,deep+1);
return wpl;
}② 基于层次遍历的算法
#define MaxSize 100 // 设置队列的最大容量
int wpl_LevelOrder(BiTree root){
BiTree q[MaxSize]; // 声明队列,end1为头指针,end2为尾指针
int end1, end2; // 队列最多容量MaxSize-1个元素
end1=end2=0; // 头指针指向队头元素,尾指针指向队尾的后一个元素
int wpl=0,deep=0; // 初始化wpl和深度
BiTree LastNode; // lastNode用来记录当前层的最后一个结点
BiTree newlastNode; // newlastNode用来记录下一层的最后一个结点
lastNode=root; // lastNode初始化为根结点
newlastNode=NULL; // newlastNode初始化为空
q[end2++]=root; // 根结点入队
while(en1!=end2){ // 层次遍历,若队列不空则循环
BiTree t=q[en1++]; //拿出队列中的头一个元素
if(t->lchild==NULL&&t->rchild==NULL){
wpl+=deep*t->weight;
} // 若为叶结点,则统计wpl
if(t->lchild!=NULL){ // 若非叶结点,则让左结点入队
q[end2++]=t->lchild;
newlastNode=t->lchild;
} // 并设下一层的最后一个结点为该结点的左结点
if(t->rchild!=NULL){ // 处理叶结点
q[end2++]=t->rchild;
newlastNode=t->rchild;
}
if(t==lastNode){ // 若该结点为本层最后一个结点,则更新lastNode
lastNode=newlastNode;
deep+=1; // 层数加 1
}
}
return wpl; // 返回wpl
}注意:当 static 关键字用于代码块内部的变量声明时,用于修改变量的存储类型,即从自动变量修改位静态变量,但变量的链接属性和作用域不受影响。用这种方式声明的变量在程序执行之前创建,并在程序的整个执行期间一直存在,而不是每次在代码块开始执行时创建在代码块执行完毕后销毁。也就是说,它保持局部变量内容的持久。静态局部变量的生存期虽然为整个源程序,但其作用域仍与局部变量相同,即只能在定义该变量的函数内使用该变量。退出该函数后,尽管该变量还继续存在,但不能使用它。
**【2015 统考真题】**用单链表保存 m 个整数,结点的结构为
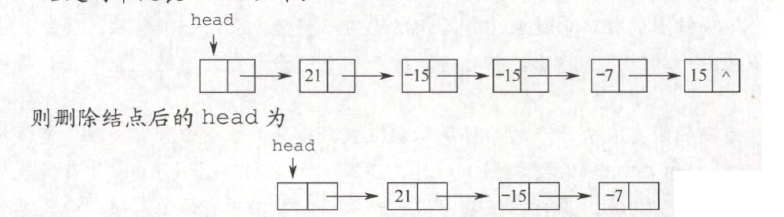
1)给出算法的基本设计思想。
2)使用 C 或 C++ 语言,给出单链表结点的数据类型定义。
3)根据设计思想,采用 C 或 C++ 或 Java 语言描述算法,关键之处给出注释。
4)说明你所设计算法的时间复杂度和空间复杂度。
【解答】
1)算法的基本设计思想:
- 算法的核心思想是用空间换时间。使用辅助数组记录链表中已出现的数值,从而只需对链表进行一趟扫描。
- 因为 |data|≤n,故辅助数组 q 的大小为 n+1,各元素的初值均为 0,依次扫描链表中的各结点,同时检查 q[|data|] 的值,若为 0 则保留该结点,并令 q[|data|]=1,;否则将该结点从链表中删除。
2)使用 C 语言描述的单链表结点的数据类型定义:
typedef struct node {
int data;
struct node *link;
}NODE;
Typefef NODE *PNODE;3)算法实现如下:
void func(PNODE h, int n){
PNODE p=h,r;
int *q,m;
q=(int *)malloc(sizeof(int)*(n+1)); // 申请n+1个位置的辅助空间
for(int i=0;i<n+1;i++) // 数组元素初值置0
*(q+i)=0;
while(p->link!=NULL){
m=p->link->data>0?p->link->data:-p->link->data;
if(*(q+m)==0){ // 判断该结点的data是否出现过
*(q+m)=1; // 首次出现
p=p->link; // 保留
}
else{ // 重复出现
r=p->link; // 删除
p->link=r->link;
free(r);
}
}
free(q);
}4)该算法的时间复杂度为
**【2017 统考真题】**请设计一个算法, 将给定的表达式树(二叉树)转换为等价的中缀表达式(通过括号反映操作符的计算次序)并输出。例如,当下列两棵表达式树作为算法的输入时:
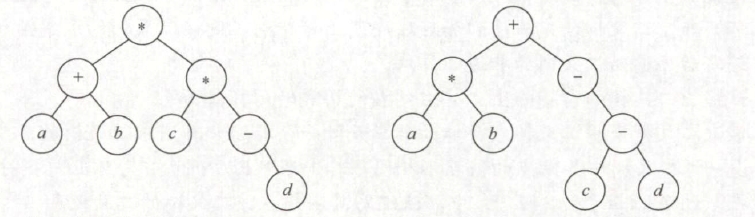
输出的等价中缀表达式分别为 (a+b)*(c*(-d)) 和 (a*b)+(-(c-d))。
二叉树结点定义如下:
typedef struct node{
char data[10];
struct node *left,*right;
}BTree;要求:
1)给出算法的基本设计思想。
2)根据设计思想,采用 C 或 C++ 或 Java 语言描述算法,关键之处给出注释。
【解答】
1)算法基本设计思想。
表达式树的中序序列加上必要的括号即为等价的中缀表达式。可以基于二叉树的中序遍历策略得到所需的表达式。
表达式树中分支结点所对应的子表达式的计算次序,由该分支结点所处的位置决定。为得到正确的中缀表达式,需要在生成遍历序列的同时,在适当位置增加必要的括号。显然,表达式的最外层(对应根结点)和操作数(对应叶结点)不需要添加括号。
2)算法实现。
将二叉树的中序遍历递归算法稍加改造即可得本题的答案。除根结点和叶结点外,遍历到其他结点时在遍历其左子树之前加上左括号,遍历完右子树后加上右括号。
void BtreeToE(BTree *root){
BtreeToExp(root,1); // 根的高度为1
}
void BtreeToExp(BTree *root, int deep){
if(root==NULL) retrun; // 空结点返回
else if(root->left==NULL&&root->right==NULL) // 若为叶结点
printf("%s",root->data); // 输出操作数,不加括号
else{
if(deep>1) printf("("); // 若有子表达式则加层括号
BtreeToExp(root->left,deep+1);
printf("%s",root->data); // 输出操作符
BtreeToExp(root->right,deep+1);
if(deep>1) printf(")"); // 若有子表达式则加1层括号
}
}**【2018 统考真题】**给定一个含 n(n≥1) 个整数的数组,请设计一个在时间上尽可能高效的算法,找出数组中未出现的最小正整数。例如,数组 {-5, 3, 2, 3} 中未出现的最小正整数是 1;数组 {1, 2, 3} 中未出现的最小正整数是 4。要求:
1)给出算法的基本设计思想;
2)根据设计思想,采用 C 或 C++ 或 Java 语言描述算法,关键之处给出注释。
3)说明你所设计算法的时间复杂度和空间复杂度。
【解答】
1)算法的基本设计思想:
要求在时间上尽可能高效,因此采用空间换时间的办法。分配一个用于标记的数组 B[n],用来记录 A 中是否出现了 1~n 中的正整数,B[0] 对应正整数 1,B[n-1] 对应正整数 n,初始化 B 中全部为 0,。由于 A 中含有 n 个整数,因此可能返回的值是 1~n+1,当 A 中 n 个数恰好为 1~n 时 返回 n+1,。当数组 A 中出现了小于等于 0 或大于 n 的值,可以不采取任何操作。
经过以上分析可以得出算法流程:从 A[0] 开始遍历 A,若 0<A[i]<n,则令 B[A[i]-1]=1;否则不做操作。对 A 遍历结束后,开始遍历数组 B,若能查找到第一个满足 B[i]==0 的下标 i,返回 i+1 即为结果,此时说明 A 中未出现的最小正整数在 1~n 之间。若 B[i] 全部不为 0,返回 i+1(跳出循环时 i=n,i+1 等于 n+1),此时说明 A 中未出现的最小正整数是 n+1。
2)算法实现:
int findMissMin(int A[], int n){
int i, *B; // 标记数组
B=(int *)malloc(sizeof(int)*n); // 分配空间
memset(B,0,sizeof(int)*n); // 赋初值为0
for(i=0, i<n; i++)
if(A[i]>0&&A[i]<=n) // 若A[i]介于1~n,则标记数组B
B[A[i]-1]=1;
for(i=0,i<n; i++) // 扫描数组B,找到目标值
if(b[i]==0) break;
return i+1; // 返回结果
}3)时间复杂度:遍历 A 一次,遍历 B 一次,两次循环内操作步骤为
**【2019 统考真题】**设线性表
typedef struct node{
int data;
struct node *next;
}NOde;请设一个空间复杂度为
1)给出算法的基本设计思想。
2)根据设计思想,采用 C 或 C++ 或 Java 语言描述算法,关键之处给出注释。
3)说明你所设计算法的时间复杂度和空间复杂度。
【解答】
1)算法的基本设计思想
先观察
① 先找出链表 L 的中间结点,为此设置两个指针 p 和 q,指针 p 每次走一步,指针 q 每次走两步,当指针 q 到达链尾时,指针 p 正好在链表的中间结点;
② 然后将 L 的后半段结点原地逆置。
③ 从单链表前后两端中依次各取一个结点,按要求重排。
2)算法实现
void change_list(NODE *h){
NODE *p,*q,*r,*s;
p=q=h;
while(q->next!=NULL){ // 寻找中间结点
p=p->next; // p走一步
q=q->next;
if(q->next!=NULL) q=q->next; // q走两步
}
q=p->next; // p所指结点为中间结点,q为后半段链表的首结点
p->next =NULL;
while(q!=NULL){ // 将链表后半段逆置
r=q->next;
q->next=p->next;
p->next=q;
q=r;
}
s=h->next; // s指向前半段的第一个数据结点,即插入点
q=p->next; // q指向后半段的第一个数据结点
p->next=NULL;
while(q!=NULL){ // 将链表后半段的结点插入到指定位置
r=q->next; // r指向后半段的下一个结点
q->next=s->next; // 将q所指结点插入到s所指结点之后
s->next=q;
s=q->next; // s指向前半段的下一个插入点
q=r;
}
}3)第 1 步找中间结点的时间复杂度为
**【2020 统考真题】**定义三元组 (a, b, c) (a,b,c 均为整数)的距离 D =|a-b|+|b-c|+|c-a|。给定 3 个非空整数集合 S1、S2 和 S3,按升序分别存储在 3 个数组中。请设计一个尽可能高效的算法,计算并输出所有可能的三元组 (a, b, c) (
1)给出算法的基本设计思想。
2)根据设计思想,采用 C 或 C++ 或 Java 语言描述算法,关键之处给出注释。
3)说明你所设计算法的时间复杂度和空间复杂度。
【解答】
分析。由 D =|a-b|+|b-c|+|c-a| ≥ 0 有如下结论。
① 当 a=b=c 时,距离最小。
② 其余情况。不失一般性,假设 a≤b≤c,观察下面的数轴:
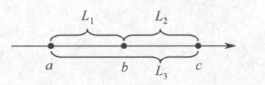
由 D 的表达式可知,事实上决定 D 大小的关键是 a 和 c 之间的距离,于是问题就可以简化为每次固定 c 找一个 a,使得
1)算法的基本设计思想
① 使用
② 集合 S1、S2 和 S3 分别保存在数组 A、B、C 中。数组的下标变量 i=j=k=0,当 i<|S1|、j<|S2| 且 k<|S3| 时(|S| 表示集合 S 中的元素个数),循环执行下面的 a)~ c)。
a)计算 (A[i], B[j], C[k]) 的距离 D;(计算 D)
b)若
c)将 A[i]、B[j]、C[k] 中的最小值的下标 +1;(对照分析:最小值为 a,最大值为 c,这里 c 不变而更新 a,试图寻找更小的距离 D)
③ 输出
2)算法实现:
#define INT_MAX 0x7fffffff
int abs_(int a){// 计算绝对值
if(a<0) return -a;
else return a;
}
bool xls_min(int a, int b, int c){// a是否是三个数中的最小值
if(a<=b && a<=c) return true;
return false;
}
int findMinofTrip(int A[], int n, int B, int m, int C[], int p){
// D_min 用于记录三元组的最小距离,初值赋为 INT_MAX
int i=0, j=0, k=0, D_min=INT_MAX, D;
while(i<n && j<m && k<p && D_min>0){
D=abs_(A[i]-B[j])+abs_(B[j]-C[k])+abs_(C[k]-A[i]);// 计算D
if(D<D_min) D_min=D; // 更新 D
if(xls_min(A[i],B[j],C[k])) i++; // 更新a
else if(xls_min(B[j],C[k],A[i])) j++;
else k++;
}
return D_min;
}3)设
**【2021 统考真题】**已知无向连通图 G 由顶点集 V 和边集 E 组成,|E|>0,当 G 中度为奇数的顶点个数为不大于 2 的偶数时,G 存在包含所有边且长度为 |E| 的路径(称为 EL 路径)。设图 G 采用邻接矩阵存储,类型定义如下:
typedef struct{ // 图的定义
int numVertices, numEdges; // 图中实际的顶点数和边数
char VerticesList[MAXV]; // 顶点表。MAXV为已定义常量
int Edge[MAXV][MAXV]; // 邻接矩阵
}MGraph;请设计算法 int IsExistEl(MGraph G),判断 G 是否存在 EL 路径,若存在,则返回 1,否则返回 0。要求:
1)给出算法的基本设计思想。
2)根据设计思想,采用 C 或 C++ 或 Java 语言描述算法,关键之处给出注释。
3)说明你所设计算法的时间复杂度和空间复杂度。
【解答】
1)算法的基本设计思想
本算法题属于送分题,题干已经告诉我们算法的思想。对于采用邻接矩阵存储的无向图,在邻接矩阵的每一行(列)中,非零元素的个数为本行(列)对应顶点的度。可以依次计算连通图 G 中各顶点的度,并记录为奇数的顶点个数,若个数为 0 或 2,则返回 1,否则返回 0。
2)算法实现
int IsExistEL(MGraph G){
// 采用邻接矩阵存储,判断图是否存在EL路径
int degree, i, j, count=0;
for(i=0;i<G.numVertices;i++){
degree=0;
for(j=0,j<G.numVertices;j++)
degree+=G.Edge[i][j]; // 依次计算各个顶点的度
if(degrree%2!=0)
count++; // 对度为奇数的顶点计数
}
if(count==0 || count ==2)
return 1; // 存在EL路径,返回1
else
return 0; // 不存在EL路径,返回0
}3)时间复杂度和空间复杂度
算法需要遍历整个邻接矩阵,所以时间复杂度是
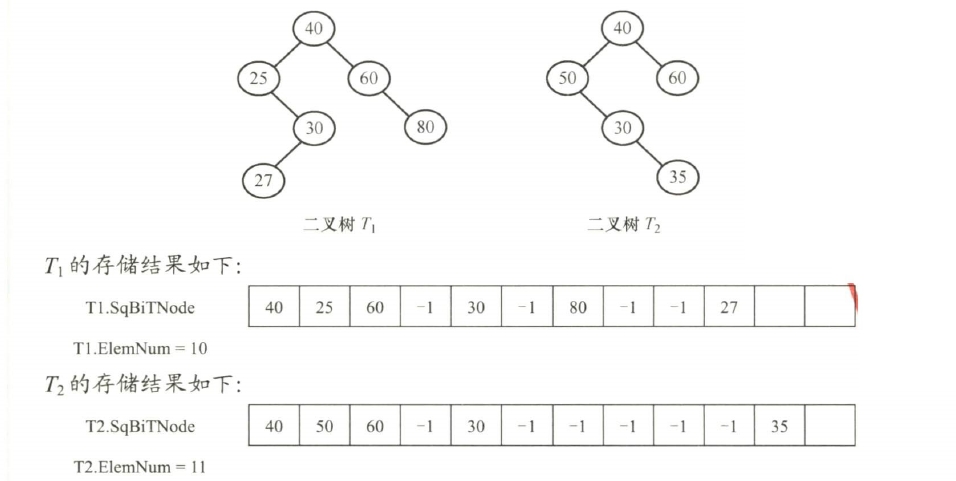
**【2022 统考真题】**已知非空二叉树 T 的结点值均为正整数,采用顺序存储方式保存,数据结构定义如下:
typedef struct{ // MAX_SIZE 为已定义常量
int SqBiTNode[MAX_SIZE]; // 保存二叉树结点值的数组
int ElemNum; // 实际占用的数组元素个数
}SqBiTree;T 中不存在的结点在数组 SqBiTNode 中用 -1 表示。例如,对于下图所示的两棵非空二叉树 T1 和 T2,
请设计一个尽可能高效的算法,判定一棵采用这种方式存储的二叉树是否为二叉搜索树,若是,则返回 true,否则,返回 false。要求:
1)给出算法的基本设计思想。
2)根据设计思想,采用 C 或 C++ 或 Java 语言描述算法,关键之处给出注释。
【解答 1】
1)算法的基本设计思想。
对于采用顺序存储方式保存的二叉树,根结点保存在 SqBiTNode[0] 中;当某结点保存在 SqBiTNode[i] 中时,若有左孩子,则其值保存在 SqBiTNode[2i+1] 中;若有右孩子则其值保存在 SqBiTNode[2i+2] 中;若有双亲结点,则其值保存在 SqBiTNode[(i-1)/2] 中。
二叉搜索树需要满足的条件是:任意一个结点值大于其左子树中的全部结点值,小于其右子树中的全部结点值。中序遍历二叉搜索树得到一个升序序列。
使用整型变量 val 记录中序遍历过程中已遍历结点的最大值,初值为一个负整数。若当前遍历的结点值小于或等于 val,则算法返回 false,否则,将 val 的值更新为当前结点的值。
2)算法实现。
#define false 0
#define true 1
typedef int bool;
bool judgeInOrderBST(SqBiTNode bt, int k, int *val){// 初始调用时k的值为0
if(k<bt.ElemNum && bt.SqBiTNode[k]!=-1){
if(!judegeInOrderBST(bt,2*k+1,val)) return false;
if(bt.SqBiTNode[k]<=*val) return false;
*val=bt.SqBiTNode[k];
if(!judgeInOrderBST(bt,2*k+2,val)) return false;
}
return true;
}【解答 2】
1)算法的基本设计思想。
对于采用顺序存储方式保存的二叉树,根结点保存在 SqBiTNode[0] 中;当某结点保存在 SqBiTNode[i] 中时,若有左孩子,则其值保存在 SqBiTNode[2i+1] 中;若有右孩子则其值保存在 SqBiTNode[2i+2] 中;若有双亲结点,则其值保存在 SqBiTNode[(i-1)/2] 中。
二叉搜索树需要满足的条件是:任意一个结点值大于其左子树中的全部结点值,小于其右子树中的全部结点值。设置两个数组 pmax 和 pmin。根据二叉搜索树的定义,SqBiTNode[i] 中的值应该大于以 SqBiTNode[2i+1] 为根的子树中的最大值(保存在 pmax[2i+1] 中),小于以 SqBiTNode[2i+2] 为根的子树中的最小值(保存在 pmin[2i+1]中)。初始时,用数组 SqBiTNode 中前 ElemNum 个元素的值对数组 pmax 和 pmin 初始化。
在数组 SqBiTNode 中从后向前扫描,扫描过程中逐一验证结点与子树之间是否满足上述的大小关系。
2)算法实现。
#define false 0
#define true 1
typedef int bool;
bool judgeBST(SqBiTNode bt){
int k,m,*pmin,*pmax;
pmin=(int *)malloc(sizeof(int)*(bt.ElemNum));
pmax=(int *)malloc(sizeof(int)*(bt.ElemNum));
for(k=0,k<bt.ElemNum;k++) // 辅助数组初始化
pmin[k]=pmax[k]=bt.SqBiTNode[k];
for(k=bt.ElemNum-1;k>0;k--){ // 从最后一个叶结点向根遍历
if(bt.SqBiTNode[k]!=-1){
m=(k-1)/2; // 双亲
if(k%2==1&&bt.SqBiTNode[m]>pmax[k]) // 其为左孩子
pmin[m]=pmin[k];
else if(k%2==0&&bt.SqBiTNode[m]<pmin[k]) // 其为右孩子
pmax[m]=pmax[k];
else return false;
}
}
return true;
}